Convolution Explained

Convolution

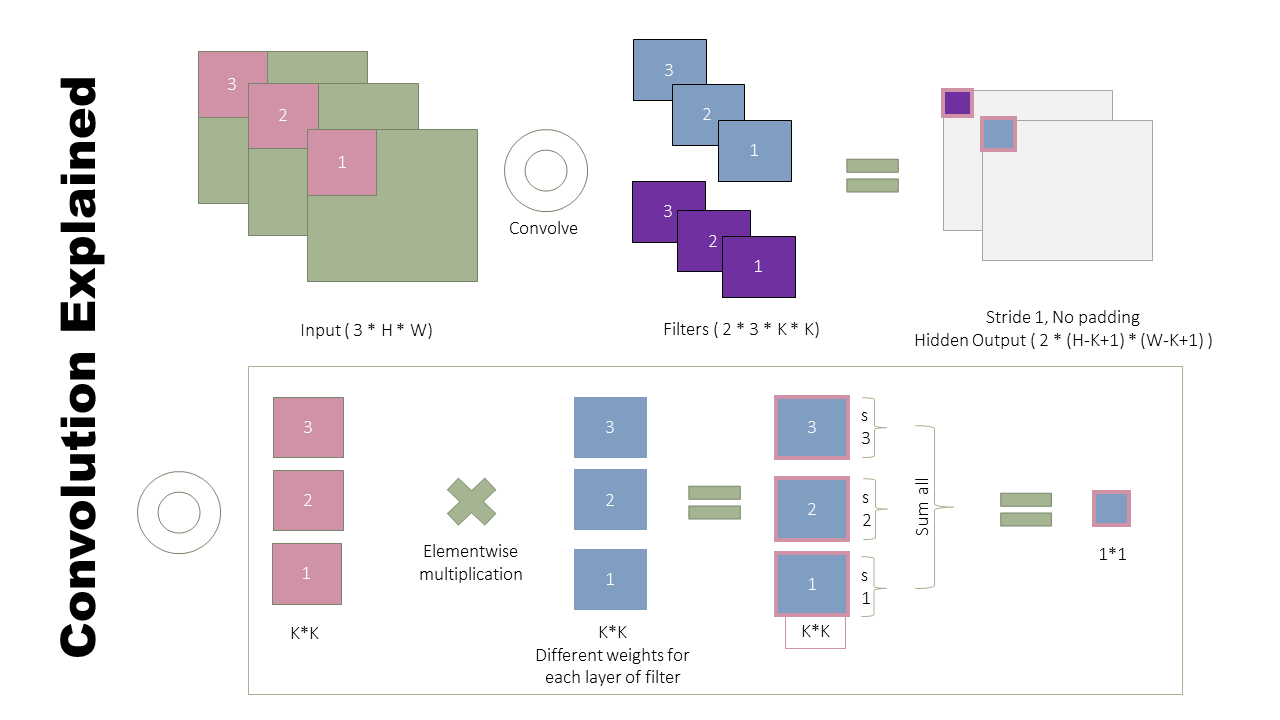
Convolution is the building block of Convolutional Neural Networks (CNN). CNNs are used both for image and text processing. Online diagrams do a great job explaining CNNs. I, however failed to find a good diagram with explanation of the convolution operation. This diagram aims to explains the details of convolution operation in a neural networks. I have also provided python scripts explaining details of the convolution operation inside pytorch.

Convolution explained

Explanation of CNN : https://en.wikipedia.org/wiki/Convolutional_neural_network#Convolutional

Let’s get into the Math

This is a 1D convolution example. The diagram above explains 2D convolution. There will be reduction in one dimension both for the filter and input.

import torch

Apply pytorch convolution

kernel_size=4 #the filter spans these many tokens at once.
max_input_length = 11
input_channels = 2 #Embedding depth
output_channels = 3
number_of_examples = 1

data = torch.randn((number_of_examples, input_channels ,max_input_length))
conv = torch.nn.Conv1d(input_channels, output_channels, kernel_size)
print(data)
cd = conv(data)
mp = torch.nn.MaxPool1d(2)
mpcd = mp(cd)

print('conv output = ',cd)

print('maxpool = ', mpcd)
print('\nInput shape = {}.\nConvolution output shape = {}\nMaxpool output shape = {}'.format(data.shape, cd.shape, mpcd.shape))

tensor([[[ 0.1239,  0.5952,  1.0756, -2.2702,  1.6780,  0.0190,  0.4516,
           0.4840, -0.0495, -0.4430, -0.4189],
         [-0.9282,  0.4426,  1.2979,  1.0455, -1.7439, -0.7124, -1.0452,
           0.8563, -0.6842,  0.9176, -0.3238]]])
conv output =  tensor([[[ 0.1685,  0.0135, -0.1587, -0.5499,  1.1779,  0.1952,  0.6602,
           0.2691],
         [ 0.5304, -0.3837, -0.2284,  1.5512, -0.1850,  0.7031, -0.0674,
           0.1530],
         [-1.0494,  2.0614, -0.5140,  0.4273, -1.5438, -0.4942, -0.6291,
           0.0829]]], grad_fn=<SqueezeBackward1>)
maxpool =  tensor([[[ 0.1685, -0.1587,  1.1779,  0.6602],
         [ 0.5304,  1.5512,  0.7031,  0.1530],
         [ 2.0614,  0.4273, -0.4942,  0.0829]]], grad_fn=<SqueezeBackward1>)

Input shape = torch.Size([1, 2, 11]).
Convolution output shape = torch.Size([1, 3, 8])
Maxpool output shape = torch.Size([1, 3, 4])

Extract parameters

All the filter weights are different for different input and output layers

params = [param for param in conv.parameters()]
print ('W(params[0]),B(params[1]) = ',[p.shape for p in params])
print(params)

W(params[0]),B(params[1]) =  [torch.Size([3, 2, 4]), torch.Size([3])]
[Parameter containing:
tensor([[[ 0.0707, -0.2901, -0.3524, -0.0037],
         [-0.2905, -0.1704, -0.0577,  0.2452]],

        [[-0.2023,  0.2368,  0.1679, -0.2610],
         [-0.0565, -0.1940, -0.0979, -0.3149]],

        [[-0.0693,  0.2306, -0.2638,  0.1681],
         [ 0.3357,  0.3071,  0.1310, -0.2856]]], requires_grad=True), Parameter containing:
tensor([ 0.3274,  0.1311, -0.2084], requires_grad=True)]

Verify by applying kernel weights manually

This step should produce same first output as conv(data)

mul = data[:,:,:kernel_size]* params[0]#W for all output channels
mul=mul.data.squeeze() #output_channel, input channel, kernel_size #same as params

print('multiplication output shape = ',mul.shape)
print('summing across all dimensions except output channel' )
#sum across kernel size and channels 
mul.sum(dim=(1,2))+params[1] #B for all output channels

multiplication output shape =  torch.Size([3, 2, 4])
summing across all dimensions except output channel

tensor([ 0.1685,  0.5304, -1.0494], grad_fn=<AddBackward0>)

Hence Conv layer sums across both input channels and kernel size for one kernel filtering operations